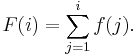Pseudo-random number sampling

Pseudo-random number sampling or non-uniform pseudo-random variate generation is the numerical practice of generating pseudo-random numbers that are distributed according to a given probability distribution.

Methods of sampling a non-uniform distribution are typically based on the availability of a pseudo-random number generator producing numbers X that are uniformly distributed. Computational algorithms are then used to manipulate a single random variate, X, or often several such variates, into a new random variate Y such that these values have the required distribution.

Historically, basic methods of pseudo-random number sampling were developed for Monte-Carlo simulations in the Manhattan project; they were first published by John von Neumann in the early 1950s.

Contents 1 Finite discrete distributions 2 Continuous distributions 3 Footnotes 4 Literature

Finite discrete distributions

For a discrete probability distribution with a finite number n of indices at which the probability mass function f takes non-zero values, the basic sampling algorithm is straightforward. The interval [0, 1) is divided in n intervals [0, f(1)) , [f(1), f(1) + f(2)), ... The width of interval i equals the probability f(i). One draws a uniformly distributed pseudo-random number X, and searches for the index i of the corresponding interval. The so determined i will have the distribution f(i).

Formalizing this idea becomes easier by using the cumulative distribution function

It is convenient to set F(0) = 0. The n intervals are then simply [F(0), F(1)), [F(1), F(2)), ..., [F(n − 1), F(n)). The main computational task is then to determine i for which F(i − 1) ≤ X < F(i).

This can be done by different algorithms:

• Linear search, computational time linear in n.
• Binary search, computational time goes with log n.
• Indexed search,^[1] also called the cutpoint method.^[2]
• Alias method, computational time is constant, using some pre-computed tables.
• There are other methods that cost constant time.^[3]

Continuous distributions

Generic methods:

• Rejection sampling
• Inverse transform sampling
• Slice sampling
• Ziggurat algorithm, for monotonously decreasing density functions
• Convolution random number generator, not a sampling method in itself: it describes the use of arithmetics on top of one ore more existing sampling methods to generate more involved distributions.

For generating a normal distribution:

• Box–Muller transform
• Marsaglia polar method

For generating a Poisson distribution:

• See Poisson distribution#Generating Poisson-distributed random variables

Footnotes

Literature

• Devroye, L. (1986) Non-Uniform Random Variate Generation. New York: Springer
• Fishman, G.S. (1996) Monte Carlo. Concepts, Algorithms, and Applications. New York: Springer
• Hörmann, W.; J Leydold, G Derflinger (2004)Automatic Nonuniform Random Variate Generation. Berlin: Springer.
• Knuth, D.E. (1997) The Art of Computer Programming, Vol. 2 Seminumerical Algorithms, Chapter 3.4.1 (3rd edition).
• Ripley, B.D. (1987) Stochastic Simulation. Wiley.